『速さ』の問題は、３つのポイントを押さえよう！

５年生で学習する『速さ』の単元では、”速さ”を求める問題の他に、”時間”や”道のり”を求める問題があります。

また、速さにも時速・分速・秒速など単位が異なるものもあり、より問題が複雑になり子どもたちを苦しめます。

そこで、速さの問題を解く上で、困ってしまいがちなところとそれを解決するための３つのポイント。それと、代表的なややこしい問題の解き方を一つ紹介します。

「速さ」がよくわからない

　算数は、覚えることがとても少ない教科です。（記憶力が悪い私は、ここが大好きです。）その数少ない覚えなければならないことに、『定義』があります。『速さとは、どういうものなのか』ということです。ここが、曖昧だと、問題を考えるときに致命的に困ってしまいます。逆にいうと、ここをしっかりと理解してイメージを持てるようになっていると、問題を自力で解決できることにつながります。

これをイメージできるように噛み砕くと、

このように『時速』について色々と広げて考えると、理解が深まりイメージできるようになります。イメージできるということは、その考え方が自分のものになり、使えるようになることだと思います。

式がたてられない

　速さの問題には、速さ・時間・道のりのいずれかを求める３通りの問題があります。

　これらの３つの公式を覚えるために

　を使う、という話をよく聞きます。

でも、先ほどの『速さ』が何かをきちんと理解しイメージできれば、公式なんか覚えなくても式は立てられます。

公式を忘れても、自分で式を作り出すことができます。

問題文の中に小数や分数が出てくると、イメージすることが難しくなりがちです。そういう時は、簡単な整数に置き換えて式を作って考えると良いです。このことについては、また別の回に書きたいと思います。

時間の単位変換が難しい

速さの問題でイヤなところは、問題文の中の数値の単位がそろっていないことが多いということです。

『時速９００キロメートルの飛行機と秒速３４０mの音の速さでは、どちらが速いでしょう。』

のような問題です。

上の問題は、速さの単位時間は時速と秒速で違いますし、速さの道のりもkmとmで違います。ですから、両方の単位をそろえる必要があります。

どちらからそろえても構いませんが、できるだけ小数より整数で計算できる方が楽かと思います。

ここでは道のりの単位をmに、単位時間の単位を秒にして、秒速何mになるかでそろえていきます。

まず、１km＝１０００mなので、時速９００kmは、時速９０００００m。

次に単位時間をそろえます。1時間は６０分。１分は６０秒ということは、必ず覚えておかなければいけません。うっかりすると、１００で割ったりかけたりしてしまうことがあります。

1時間に９００００００mということは、６０分で９０００００m進むということなので、１分でどれだけ進むかを考えるには、

９０００００➗６０＝１５０００　分速１５０００m

１分間に１５０００mということは、６０秒で１５０００m進むということなので、１秒間でどれだけ進むかを考えるには、

１５０００➗６０＝２５０　秒速２５０m

慣れてくれば、1時間は６０✖️６０＝３６００　３６００秒

なので、９０００００➗３６００＝２５０　秒速２５０m

と計算することもできます。

よって、答えは　音の方が速い　となります。

電車がトンネルを通過する問題が解けない

速さに単元の終わりの方に出てくる問題です。なかなか厄介ですね。

① まず、電車が進んだ距離は、電車の先頭に旗🚩があると考えるとわかりやすいと思います。トンネルの入り口から、列車が完全にトンネルを出るまでなので（下の絵参照）

１２００＋６０＝１２６０　　１２６０m

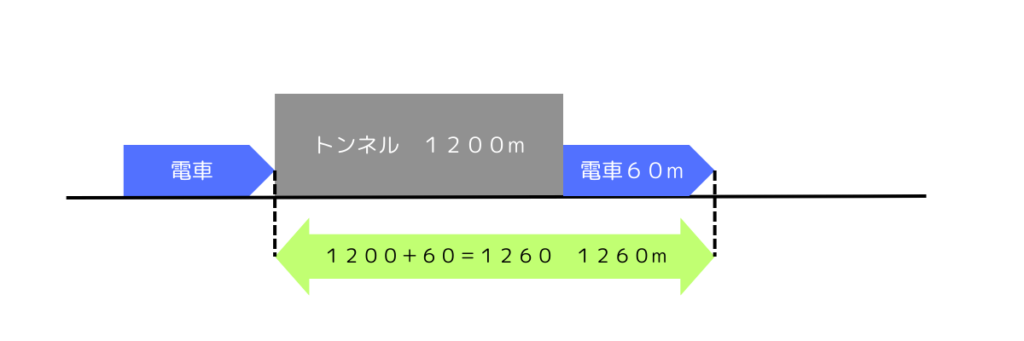
②　次に、時速１２６kmの単位を秒速⚪︎mに直します。

　１km＝１０００mなので、１２６km＝１２６０００m

　1時間は、６０✖️６０＝３６００秒なので、

　３６００秒で１２６０００m進む速さということです。

　１秒でどれだけ進むか考えると、

　１２６０００➗３６００＝３５

　秒速３５mとなります。

　１秒で３５m進むので、１２６０m進むのにかかる時間は、

　１２６０➗３５＝３６

　答え　３６秒　となります。

算数・数学全般に言えることですが、定義をしっかりと理解し、イメージできるようにしておくことが大切です。ここが基本です。速さが何かがわからなければ、問題を解くことはできません。