文章問題で、何算を立てれば良いのか迷ってしまうことがあります。四則演算のどれを使っていいのかわからない。この原因の一つに、たし算・ひき算・かけ算・わり算は、一体どういうときに使う式なのか、それらの式の意味は何なのか、をよく理解していないことがあります。
ここでは特に、基本的な四則演算について考えてみます。
たし算・引き算・・・違いを求める問題が難しい。
たし算は、”合わせる時”や”増える時”に使います。ひき算は、”残り”や”違い”を求めるときに使います。一年生でブロックなどを実際に操作しながら、これらの4つの数量の変化を、感覚でも掴めるようにしながら学びます。
二つのブロックのかたまりを両手で合わせたり(合わせる時はたし算)、ブロックのかたまりに別のかたまりを合体させたり(増える時はたし算)、ブロックのかたまりからいくつかをよけたり(残りや違いはひき算)しながらたし算・ひき算を学びます。
これらの中でも、”違い”の考え方はお子さんにとっては難しいものです。二つの数量を並べて同じ分だけとった残りの数という考え方は、他の考え方より難易度が高いです。
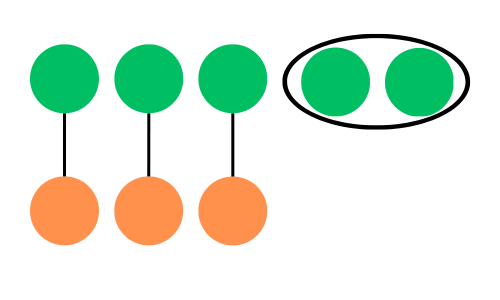
また、身の周りで”違い”を求める場面は、他の三つに比べて少ないと思います。それもあって、”違い”を求める文章問題で、ひき算をたてられないということが多いように思います。
かけ算・・・九九を覚えるだけでは式を作れない
かけ算は、2年生で学習します。子どもたちは、学校でもご家庭でも一生懸命にかけ算九九を繰り返し覚えます。全ての段の九九を覚えて一安心。ところが、実は結構すぐに忘れてしまいます。概ね覚えていても、いくつかのかけ算は出てこないとか、まちがえてしまうという事が多いです。ですので、かけ算九九は、時々復習してしっかりと定着させることが必要です。
このように、かけ算では九九を覚えることに力を入れますが、九九を覚えるだけでは、文章問題で立式はできません。実は、かけ算の意味がよく理解できていないことが多いのです。
教科書には『4の3つ分のことを 4✖️3 とかく。これを4の3倍ともいう。』と書かれています。つまり 4✖️3は、下の図のような場合の🔴の数を求める式です。

同じ数量がいくつもあるときに掛け算が使えるのです。このイメージをしっかりと持てていないと、文章問題でかけ算が立てられません。
『イチゴを一人に4つずつ配ります。3人に配るには、いちごはいくついりますか。』のような問題で、
4+4+4
にしたり(間違ってはいませんが、計算が煩雑になります)
増えるから 4+3 とか
3✖️4 としてしまったりします。
絵や図を描いて、同じものがいくつもあったらかけ算が使える。ということがイメージできるようになることが大切です。
わり算・・・全部の数量がわかっているものを同じ数ずつ分けるとき
わり算は、3年生で勉強します。割り算の単元の前に、
『5✖️⬜︎=15 ⬜︎はいくつでしょう。⬜︎は5の段の九九を唱えていって15になる数だから3』
という、⬜︎にあてはまる数を求める学習をします。
教科書には、わり算になる2つの場合について書かれています。
① 12こを3人に同じ数ずつ分けるときの一人分を求める式を、
12 ➗ 3 = 4 とかく。
全部の数 人数 一人分の数
かけ算にすると、
一人分の数 ✖️ 3 = 12
12➗3の答えは、
⬜︎ ✖️ 3 =12 の⬜︎にあてはまる数と同じ。
② 12このあめを一人に3こずつ分けると何人に分けられますか
3こずつ何人かに分けてあげたら、全部で12こということなので、かけ算で表すと
3 ✖️ 人数 = 12
3✖️⬜︎=12 の⬜︎にあてはまる数。
⬜︎は、3の段の九九で求められる。
これも割り算で表し、
12 ➗ 3 = 4 と書く。
全部の数 一人分の数 人数
まとめ 一人分の数を求めるときも、何人に分けられるかを求める時も、わり算の式になる。
わり算の答えは、わる数の段の九九を使って求められる。
授業では、両方の考え方についてブロックを操作しながら学びます。
これらの教科書に書いてあることをまとめると、
全部の数量がわかっているものを同じ数ずつ分けるときの、
・一つ分がいくつになるか。
・いくつに分けられるか。
を求めるときには、わり算を使う。
ということがわかります。例えば、
例 🔴 が12こあります。これを同じ数ずつに分けます。

・ 一皿分の🔴は、いくつですか。とか、
・ お皿はいくつになりますか。
(いくつに分けられますか。)
を求めるときには、わり算にする。ということになります。
まとめ・・・生活の中で楽しく数字と関わって、式のイメージを身につけよう
四則演算の基本的なイメージをしっかりと持つことは、非常に大切です。ここが曖昧では、問題を読んで式を立てることは難しいです。これは、授業で学んだだけでは十分に定着しにくいです。文章問題を解くときに絵や図をかいたりして、繰り返し具体的にイメージできるように練習する。このことが、式を立てられるようになる上でとても大切になります。
また、文章問題を考えるときには、子どもの生活体験も生かされます。自分が体験したことは、問題でイメージに結びつきやすいですし、その中で関わった数量は、数量感覚を自然とアップさせてくれると考えます。最近は、お子さんがおつかいに行って、自分でお金を払って買い物をするという機会が減ってきています。なので、お金が出てくる問題のイメージがわかない。お釣りは、自分が出したお金から代金を引いた金額だ、という経験をしたことがない、というお子さんも増えています。
体験以外にも、日頃のおしゃべりや聞いた話、読書などからも、ちょっと意識することで、数量感覚が培われ、立式の力に結びつけられると思います。手前味噌になって恐縮ですが、母が私にしてくれたことを紹介します。母は、とても算数が苦手です。(本人がそう言っています。)ですが、私が幼い頃、簡単なお話を即興で創って面白おかしく話してくれました。私は、その話を聞くのが大好きでした。一緒にお風呂に入った時に、お化けや動物が出てくる話をよくしてくれました。その中に、時々簡単な算数の問題が入っていました。『お化けが3人いました。友達のお化けが2人来ました。あれ、みんなで何人になったのかなあ?』のような簡単な物でしたが、それを考えるのがとても楽しかったことを今でも覚えています。私が算数好きになった原点は、ここにあるのではないかと思っています。
楽しみながら数字に関わると、数量の感覚も楽しく身につきやすいと思います。それは、文章問題で式を立てることにも大きく関わってきます。クイズ番組を見ながら、出てきた数について子どもに投げ返してみるとか、買い物で割引の札を見て、どのくらい安くなるのか一緒に考えてみるなど、色々な場面で数字を楽しめるといいですね。


